Carlsen - Caruana
The reigning World Chess Champion Magnus Carlsen squares off against Fabiano Caruana in The World Chess Championship Match in London starting today. As I did in 2014 and 2016, I have tried to model the probable outcomes of this year’s match.
First a bit about methodology as that has continued to evolve. In 2014 there were two different models; one based on rating alone, and one that was adjusted for the match situation. By 2016 it had evolved into one model, which incorporated previous championships into the adjusted ratings model.
This year will see the introduction of previous Carlsen - Caruana games into the model, thus giving it three distinct inputs.
Rating
Currently, Magnus Carlsen has a rating of 2835 while Fabiano Caruana is just three points behind at 2832. That is incredibly close, and all games are expected to be close. For modeling purposes, I needed to find out just how close. To find the draw rate, I analyzed approximately 300 games over the last five years in which both players were rated at least 2750 and where the difference in rating was less than 15. 70.6% of those games ended in draws, and this becomes the probable draw rate based on rating. Finally, each player's win chances are calculated based on their respective ratings after adjusting for white’s first move advantage (equivalent to about 35 points). That would yield the following probabilities per game:
| Caruana White | Carlsen White |
|
| Carlsen Win | 10.1% | 20.2% |
| Draw | 70.6% | 70.6% |
| Caruana Win | 19.3% | 9.2% |
Previous Championships
However, match situations are different and World Chess Championship Matches especially so. That’s why I further analyzed the 122 games where the initial rating difference was 40 or less. Again, I split the games based on on whether the highest rated player had the white or the black pieces. That produced the following probabilities per game, which again predicts close games but with fewer draws.
| Lower ELO White | Higher ELO White |
|
| Higher ELO Win | 12.7% | 26.6% |
| Draw | 63.5% | 62.5% |
| Lower ELO Win | 23.8% | 10.9% |
Head-to-head record
Lastly, I also wanted to incorporate the players themselves as they have played frequently. I simply decided to make their head-to-head record part of the model as well. They tend to have more decisive games than average, with Carlsen coming out on top more often.
Final model - before start
Putting all of these factors into a single model requires some weighting decisions. Since the sample sizes are much bigger with respect to rating, that counts for half of the model, while the remaining have one quarter each. That means that this year’s model uses the following probabilities for simulating each game:
| Caruana White | Carlsen White |
|
| Carlsen Win | 16.0% | 24.1% |
| Draw | 63.7% | 65.6% |
| Caruana Win | 20.3% | 10.3% |
This means that the model assumes that there is about a 2/3 chance that a game will be drawn, and the player with white will be the favorite. Compared to earlier years, this is a first for Magnus Carlsen as the previous models had him as a slight favorite even with the black pieces. However, he is still slightly favored by the model and in a match situation that helps in the end. Using these probabilities as the premise for 10 000 simulations of the match, the model thinks the championship will be decided as follows:
A close match, but Magnus Carlsen is slightly favored to retain the title as World Champion. He has a 51% chance of winning outright, compared with 30% for Caruana. There's also a 20% chance it will have to be decided by tie-break, so we could be in for a long match. In fact, the model thinks there's an 80% chance that there will be at least 11 games and will be very surprised if it is decided before the ninth game.
Compared with previous years, this promises to be a very close match. A 60/40 split can very easily tip both ways, and a win by Caruana in the first game will flip those probabilities in his favor.
Game 1
Game one of Carlsen - Caruana was a spectacular one that eventually ended in a draw. As that was the most likely outcome before start, the overall win chances did not change much. Caruana has used one of his white-games though, which slightly shifts the odds towards the reigning champion. It does not influence how long the match itself is likely to last, as it shaved a point off Caruana in game 12 in favor of Carlsen.
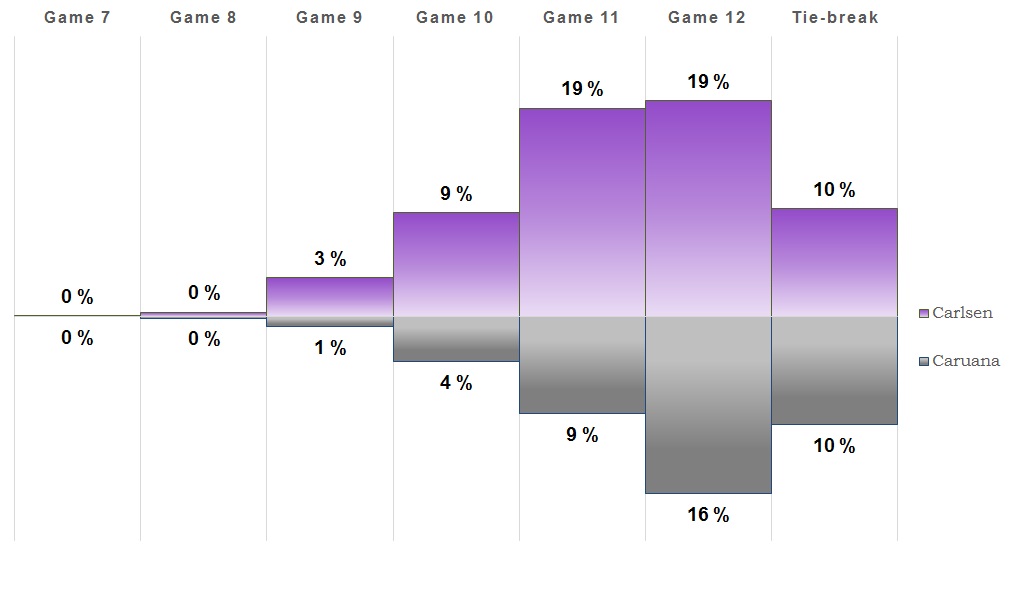
Game 2
Game two ended in another draw and once again the overall win chances did not change much. They've both used one white game each, but as Carlsen was slightly favored ahead of the match, the probabilities will move against him as long as he doesn't score. We're now at an 85% chance of at least 11 games, and this looks to be close all the way.
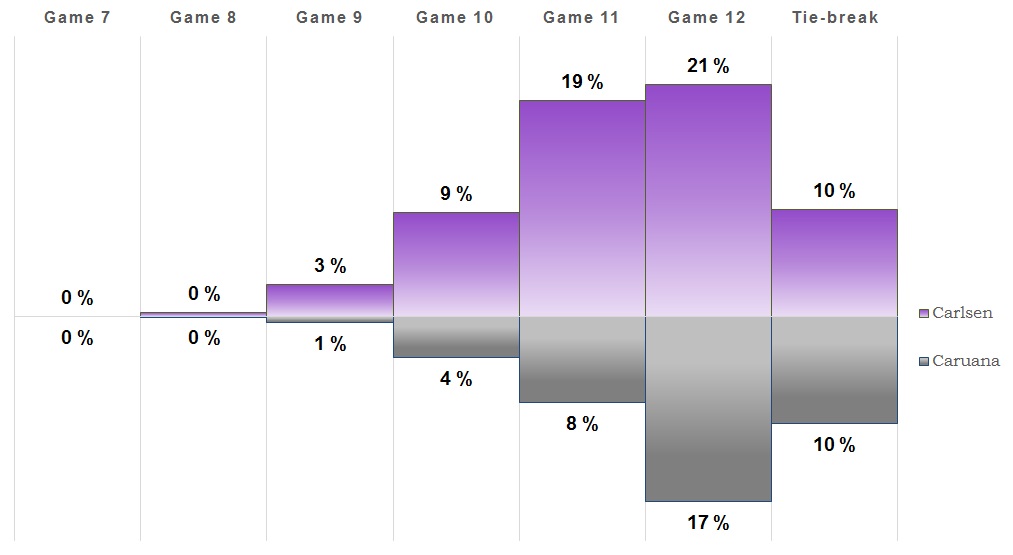
Game 3
Another draw in game three and once again the overall win chances did not change much. We'll see if tomorrow's game brings some more action.
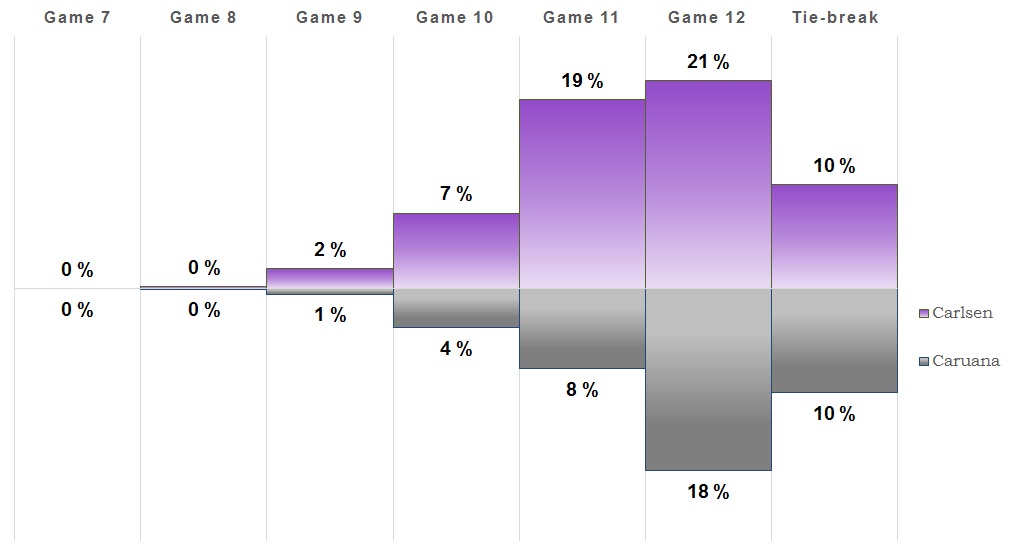
Game 4
You know the drill, another draw. As these keep coming in, the likelihood of a tie-break increases while Carlsen's chances decrease. Caruana has stayed more or less the same since the beginning of the match. We'll see if things change in game five.
Game 5
Yet another draw, and it's looking increasingly likely that it will go to at least 12 games. Getting close to the point where a tie-break is as likely as an outright Caruana win.
Game 6
We've reached half-way and it's been draws all the way so far. Seemed for a while like we might have a winner, but it's still looking like this will be fought all the way.
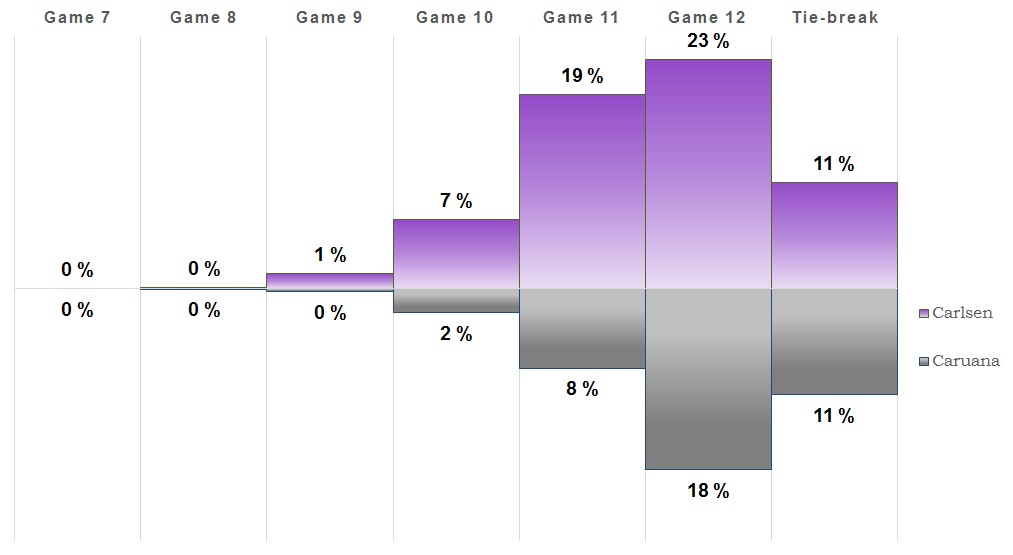
Game 7
A quick draw, and Caruana now has the most white-games left. It's looking more and more like there could be a tie-break and it's almost as likely as Caruana winning outright. Hence there was an update to the model for how to calculate win chances in the tie-break. Instead of assuming 50/50 chances, the Rapid and Blitz ratings have been used to infer the chances in a tie-break. The model assumes a roughly 2 in 3 chance of Carlsen winning and 1 in 3 of Caruana ending up victorious in a possible tie-break.1It bases this on expected score based on their ratings in rapid and blitz, where 2/3 weight is given to rapid since it's first. Carlsen is rated 91 points higher in rapid and 172 in blitz, which would give expected scores of 63% and 73% respectively, for a weighted average of 66%.
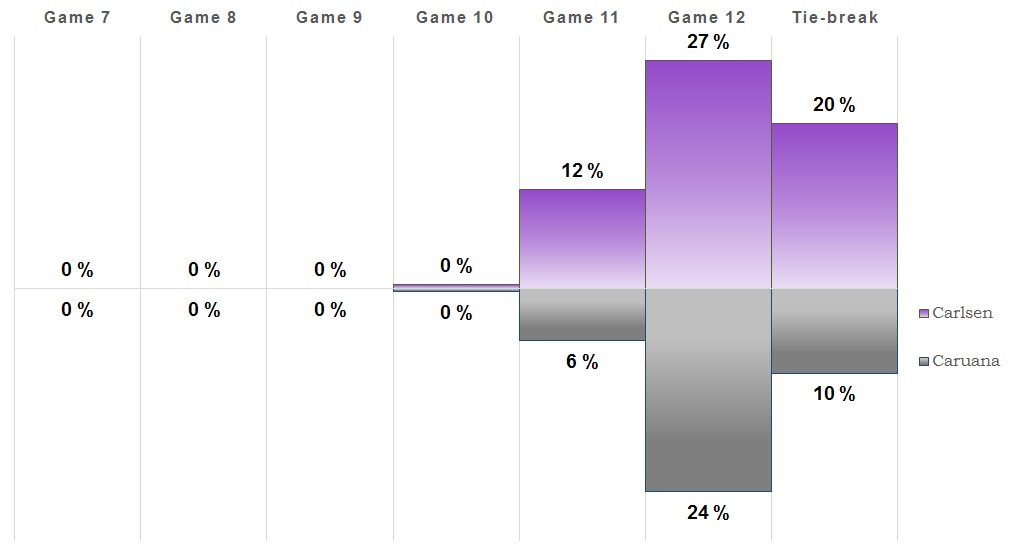
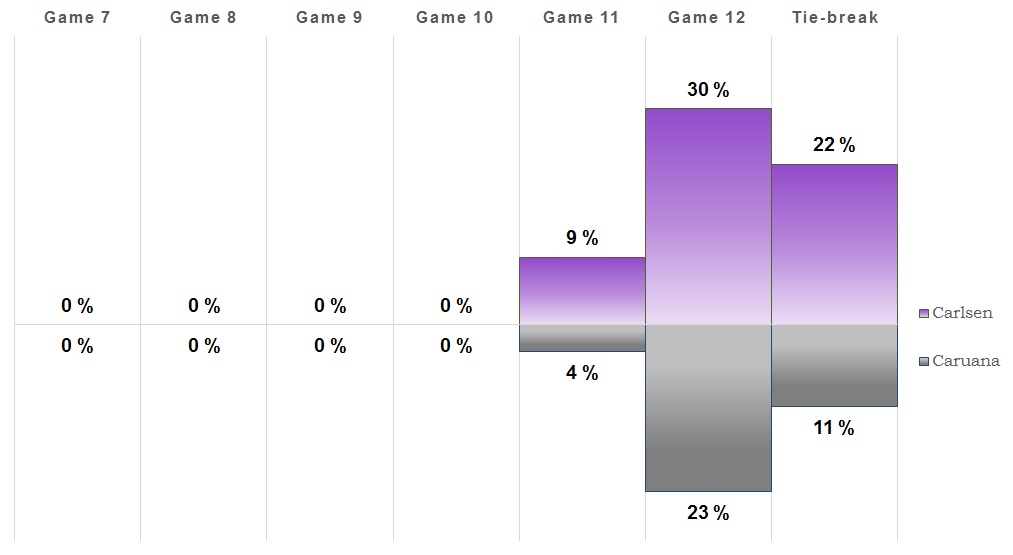
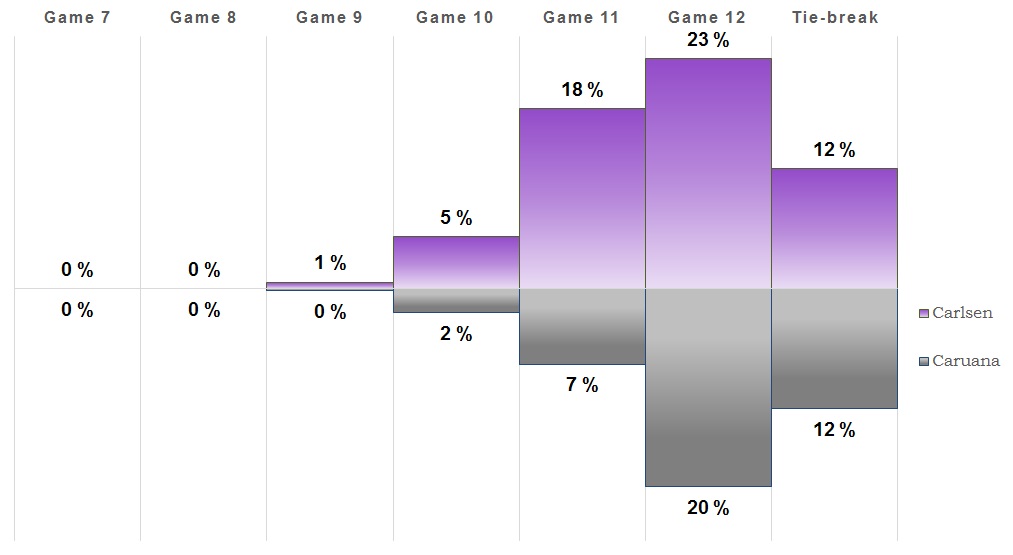
Game 8
Once again a game that saw some action but ended up with a draw. So this one goes to (at least) 11! It's also more likely that the match will be decided on tie-breaks than Caruana winning outright. We're also getting close to the point where a tie-break is the most likely outcome, but we'll see what the next game brings.